This namespace provides two dimensional algorithms. More...
This namespace provides two dimensional algorithms.
This namespace provides two dimensional algorithms. There are different classes of algorithms that generate different partition structures.
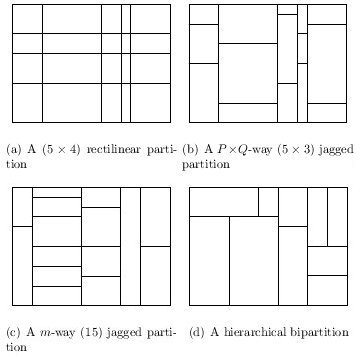
Different structures of partitions
Rectilinear partitioning algorithms are described in section 3.1, jagged partitioning algorithms are in section 3.2, hierarchical partitioning algorithms are in 3.3 and hybrid part. are in section 5 of "E. Saule, E. O. Bas, U. V. Catalyurek, Load-Balancing Spatially Located Computations using Rectangular Partitions Paper, Tech. Report, ArXiv, no. arXiv:1104.2566v1, 2011" and twod::Hybrid doucmentation. The partition structures are denoted at the prefix of each class' name. For example JagMHeurProbeBest generates jagged partition structure. We see this form Jag- prefix. The other prefixes are Hier- (Hierarchical) and Rect- (Rectilinear). Hybrid algorithms generate a combination of those structures depending on the algorithm used in each level.
Most of 2D partitioning algorithms have 3 variants based on first dimension's cut orientation. Those are denoted at the suffix of each class' name such as: xxxHor, xxxVer, xxxBest. xxxHor and xxxVer first places horizontal and vertical cuts respectively. For example JagMHeurProbeHor first creates row-wise stripes and then independently partitions each stripe. Similarly, JagMHeurProbeVer creates column stripes. xxxBest tries both orientations and returns the solution with lesser bottleneck (bottleneck refers to maximum loaded processor's load).
Optimal algorithms are provided in jagged partitioning. Those are: JagMOptBest, JagPQOptBest, JagPQOptIntervalBest (or their variants).
However, optimal algorithms can take a very long time. Therefore we recommend using effective heuristic algorithms such as JagMHeurBest or JagMHeurProbeBest (or their variants).
The solution of 2D algorithms are expressed using util::RectList and util::rectangle.
All 2D algorithms derive from PartBase class. twod::Parser::parseName() function is used to easily translate string name into proper object. All 2D algorithms use bracket notation for 2D prefix sum array as noted in util::PrefixSumArray2DOfTBracket.
Given a 2D algorithm name string, twod::Parser::parseName() returns proper partitioning algorithm object. All algorithms can be found and conveniently used in this function. If a new algorithm is implemented, it should derive from PartBase class and the algorithm may be added to twod::Parser::parseName() for easy string-to-object conversion.
Classes | |
| class | JagPQHeurHor |
| implements a PxQ jagged partitioning heuristic using the first dimension as main dimension. More... | |
| class | JagPQHeurVer |
| implements a PxQ jagged partitioning heuristic using the second dimension as main dimension. More... | |
| class | JagPQHeurBest |
| implements a PxQ jagged partitioning heuristic taking as the main dimension the one that leads to the best load balance. More... | |
| class | Hybrid |
| hybrid algorithms for 2d partitioning. A first partitioning is done with a 2d algorithm. Then, each part is partitioned during a second level using an other algorithm. More... | |
| class | JagPQOptIntervalHor |
| optimal PxQ jagged algorithm from "Ali Pinar and Cevdet Aykanat, Sparse Matrix Decomposition with Optimal Load Balancing, HiPC 1997" using the first dimension as the main dimension. More... | |
| class | JagPQOptIntervalVer |
| optimal PxQ jagged algorithm from "Ali Pinar and Cevdet Aykanat, Sparse Matrix Decomposition with Optimal Load Balancing, HiPC 1997" using the second dimension as the main dimension. More... | |
| class | JagPQOptIntervalBest |
| optimal PxQ jagged algorithm from "Ali Pinar and Cevdet Aykanat, Sparse Matrix Decomposition with Optimal Load Balancing, HiPC 1997" . It selects the main dimension to get the best possible load balance. More... | |
| class | JagMOptHor |
| An optimal m-way jagged algorithm based on dynamic programming. More... | |
| class | JagMOptVer |
| An optimal m-way jagged algorithm based on dynamic programming. More... | |
| class | JagMOptBest |
| An optimal m-way jagged algorithm based on dynamic programming. More... | |
| class | JagPQOptHor |
| an optimal PxQ-way jagged partitionning algorithm using a Dynamic Programming based algorithm. More... | |
| class | JagPQOptVer |
| an optimal PxQ-way jagged partitionning algorithm using a Dynamic Programming based algorithm. More... | |
| class | JagPQOptBest |
| an optimal PxQ-way jagged partitionning algorithm using a Dynamic Programming based algorithm. More... | |
| class | JagMHeurHor |
| implements an m-way jagged partitioning heuristic using the first dimension as the main dimension. More... | |
| class | JagMHeurVer |
| implements an m-way jagged partitioning heuristic using the second dimension as the main dimension. More... | |
| class | JagMHeurBest |
| implements an m-way jagged partitioning heuristic using as the main dimension the one that leads to the best load balance. More... | |
| class | JagMHeurProbeHor |
| Finds least max proc load value by applying binary search over it. First cut direction is horizontal. See section 3.2.2 PROBE-M algorithm of "E. Saule, E. O. Bas, U. V. Catalyurek, Load-Balancing Spatially Located Computations using Rectangular Partitions Paper, Tech. Report, ArXiv, no. arXiv:1104.2566v1, 2011". More... | |
| class | JagMHeurProbeVer |
| Finds least max proc load value by applying binary search over it. First cut direction is vertical. See section 3.2.2 PROBE-M algorithm of "E. Saule, E. O. Bas, U. V. Catalyurek, Load-Balancing Spatially Located Computations using Rectangular Partitions Paper, Tech. Report, ArXiv, no. arXiv:1104.2566v1, 2011". More... | |
| class | JagMHeurProbeBest |
| Finds least max proc load value by applying binary search over it. First cut direction is decided by tring both horizontal and vertical first dimension cuts. See section 3.2.2 PROBE-M algorithm of "E. Saule, E. O. Bas, U. V. Catalyurek, Load-Balancing Spatially Located Computations using Rectangular Partitions Paper, Tech. Report, ArXiv, no. arXiv:1104.2566v1, 2011". More... | |
| class | RectNicol |
| Implements the rectilinear partitioning algorithm with iterative refinement described in "David Nicol, Rectilinear Partitioning of Irregular Data Parallel Computations, JPDC, 1994". More... | |
| class | Parser |
| Converts text into corresponding 2D algorithm objects. More... | |
| class | PartBase |
| base class for the 2D partitioning algorithm More... | |
| class | RecBisect2D |
| implements variants of the recursive bisection algorithm originally published in "Marsha Berger and Shahid Bokhari, A Partitioning Strategy for Nonuniform Problems on Multiprocessors, IEEE TC, 1987". More... | |
| class | HierRelaxed |
| implements the hierarchical relaxed heuristic and some variants. More... | |
| class | Uniform |
| Implements the area based rectilinear of the space. More... | |
 1.7.1
1.7.1