util::PrefixSumArray1DOfTBracket< T > Class Template Reference

skeleton of prefix sum array using the bracket notation[] for 1d partitioning algorithm (this class does not actually exist). More...

#include <util/template.hpp>

---

Detailed Description

template<typename T>
class util::PrefixSumArray1DOfTBracket< T >

skeleton of prefix sum array using the bracket notation[] for 1d partitioning algorithm (this class does not actually exist).

Any type that provides the following functions can be used safely with 1D partitioning algorithms that use the bracket notation. This class does not actually exist, it is provided for documentation purpose only. Notice that since the types are given as template parameter to the partitioning algorithm, there is no need to inherit from this class.

Notice that the class does not need to provide its size since it is given as a parameter to the 1D partitioning functions.

Types that respect this prototype include: double*, int*, util::Aggreg2Dto1D.

The prefix sum array of an array of primitive type (or even some complex type) can be constructed using util::prefixsum.

List of all members.

Public Member Functions
const T &	operator[] (int i) const
	returns the i-th element of a prefix sum array.

---

Member Function Documentation

template<typename T >

const T& util::PrefixSumArray1DOfTBracket< T >::operator[]

(

int

i

)

const

returns the i-th element of a prefix sum array.

That is to say if this is the prefix sum array of array A, we have : . This enforces that the first element is null: and that the array is monotonically increasing: .

Notice that if the original array is of size 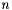then this array should be of size 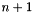. (In a sense, it is a Pascal-style array where the element at index 0 is worth 0.)

---

The documentation for this class was generated from the following file:

• include/util/template.hpp