This namespace provides multiple utilitarian classes and function used in 1D and 2D partitioning algorithm (for instance as input and output). More...

Detailed Description

This namespace provides multiple utilitarian classes and function used in 1D and 2D partitioning algorithm (for instance as input and output).

This namespace provides multiple utilitarian classes and function useful in 1D and 2D partitioning algorithm. Most notably it provides implementation of various PrefixSumArray for the 1D and 2D case which can be used as input of the partitioning algorithm. It also provides the rectangle and RectList object that constitute the output of 2D partitioning algorithms.

1D partitioning algorithms (available in oned) take as an input parameter a 1D prefix sum array that follows the bracket notation [] or the interval notation. If it follows the bracket notation, the type should implement the functions described in util::PrefixSumArray1DOfTBracket. If it follows the interval notations, the type should implement the functions described in util::PrefixSumArray1DOfTInterval.

2D partitioning algorithms (available in twod) take as an input parameter a 2D prefix sum array that follows the bracket notation []. A type that follows the bracket notation should implement the functions described in util::PrefixSumArray2DOfTBracket. Nothing prevents an algorithm to use an equivalent of the interval notation in 1D in 2D. But it never appeared useful and so never was implemented.

The solution of 2D algorithms is expressed using util::RectList and util::rectangle. Some communication related metrics can be computed with util::Comm_cost_2d.

Classes
class	Aggreg2Dto1Dpart
	This class implements the interval notation for 1d array as defined by util::PrefixSumArray1DOfTInterval. More...
class	Comm_cost_2d
	Methods to measure communication cost. More...
class	Compact2D
	Provides a 2D array of T which is compact in memory to optimize caches and memory allocations. More...
class	Compact3D
	provide three dimensional arrays which are compact in memory (for cache performance). More...
class	MProbe
	M-way partitioning algorithm feasibility check. The check is done on a set of arrays as described in section 3.2.2 of "E. Saule, E. O. Bas, U. V. Catalyurek, Load-Balancing Spatially Located Computations using Rectangular Partitions Paper, Tech. Report, ArXiv, no. arXiv:1104.2566v1, 2011" More...
class	Multiarrays
	A wrapper class to hold multiple arrays. More...
class	ParametricSearch
	contains several probe algorithms used for 1d partitioning. More...
class	Prefix2D
	a prefix sum array (2d) More...
class	Aggreg2Dto1D
	1D representation of a section of a prefix sum array by summing its element row-wise or column-wise. More...
class	AggregMax2Dto1D
	Reduces a 2D matrix with stripes into 1D dimension by returning the load of the most loaded stripe. More...
struct	rectangle
	a rectangular region (inside a matrix). More...
class	RectList
	a list of rectangle inside Pr More...
class	SubPSA
	represent a rectangular region of a prefix sum array as an prefix sum array. More...
class	PrefixSumArray1DOfTBracket
	skeleton of prefix sum array using the bracket notation[] for 1d partitioning algorithm (this class does not actually exist). More...
class	PrefixSumArray1DOfTInterval
	skeleton of prefix sum array using the interval notation for 1d partitioning algorithm (this class does not actually exist). More...
class	PrefixSumArray2DOfTBracket
	skeleton of prefix sum array using the bracket notation for 2d partitioning algorithm (this class does not actually exist). More...
class	timestamp
	allow to keep track of time with a precision of a microseconds. More...
class	TransposePrefix2D
	represents the transpose of a prefix sum array. More...
Functions
template<typename Pr >
bool	constraint_psa (const Pr &psa)
	check some properties of a 2d Prefix Sum Array.
template<typename Pr , typename output >
void	output_psa (const Pr &psa, output &out)
	outputs the load array represented by a prefix sum array.
template<typename T , typename Pr >
int	extractXDim (const util::RectList< T, Pr > &currentP, int *cuts, std::vector< int > procs[])
template<typename T , typename Pr >
int	extractXDim (const util::RectList< T, Pr > &currentP, int *cuts)
template<typename T >
void	prefixsum (const T array, T result, int length)
	Assembles 1d prefix sum array.
template<typename T , typename Pr >
int	binarySearch (const Pr &prefixSumArray, int low, int high, T prefixSumBottleneck)
	search for prefixSumBottleneck inside a sorted array between l and h
template<typename T , typename Pr >
int	binarySearch_interval (const Pr &prefixSumArray, int low, int high, T prefixSumBottleneck, int base)
	search for the largest interval rooted at base inside prefixSumArray finishing between low and high whose value is less then prefixSumBottlneck using a binary search.
template<typename T , typename Pr >
int	binarySearchLeft (const Pr &prefixSumArray, int low, int high, T prefixSumBottleneck)
	TODO: this function is un documented in doxygen.
template<typename T , typename Pr >
void	distribute_processors (const Pr &psa, const util::RectList< T, Pr > &v, std::vector< int > &alloc, int m)
	allocate processors to rectangle proportionnally to their load.
std::ostream &	operator<< (std::ostream &out, const rectangle &r)
template<typename T , typename Pr >
std::ostream &	operator<< (std::ostream &out, const util::RectList< T, Pr > &r)
int	intfactor (int x)
	finds the largest factor of a number less than its square root

Function Documentation

template<typename T , typename Pr >

int util::binarySearch	(	const Pr &	prefixSumArray,
		int	low,
		int	high,
		T	prefixSumBottleneck
	)

search for prefixSumBottleneck inside a sorted array between l and h

Parameters:

	prefixSumArray	a monotonic non-decreasing array
	low	lower bound (included)
	high	upper bound (included)
	prefixSumBottleneck	value to look for (TODO: shouldn't this parameter be a const reference)

Returns:: the largest index $low <= i <= high$ of prefixSumArray where the value prefixSumArray[i] <= prefixSumBottleneck. if prefixSumBottleneck < prefixSumArray[low] the function returns -1

template<typename T , typename Pr >

int util::binarySearch_interval	(	const Pr &	prefixSumArray,
		int	low,
		int	high,
		T	prefixSumBottleneck,
		int	base
	)

search for the largest interval rooted at base inside prefixSumArray finishing between low and high whose value is less then prefixSumBottlneck using a binary search.

uses interval notation

Parameters:

	prefixSumArray	a monotonic non-decreasing array per interval
	low	lower bound (included)
	high	upper bound (included)
	prefixSumBottleneck	value to look for
	base	beggining of the interval

Returns:: the largest index $low <= i <= high$ of prefixSumArray where the value prefixSumArray.interval(base,i) <= prefixSumBottleneck. if prefixSumBottleneck < prefixSumArray.interval(base,low) the function returns -1

template<typename T , typename Pr >

int util::binarySearchLeft	(	const Pr &	prefixSumArray,
		int	low,
		int	high,
		T	prefixSumBottleneck
	)

TODO: this function is un documented in doxygen.

template<typename Pr >

bool util::constraint_psa ( const Pr & psa )

check some properties of a 2d Prefix Sum Array.

Namely, it verifies the first row and columns are 0. That every element is positive and that the matrix is non-decreasing

Parameters:

psa

the object to test.

Returns:: true if all constraints are valid.

template<typename T , typename Pr >

void util::distribute_processors	(	const Pr &	psa,
		const util::RectList< T, Pr > &	v,
		std::vector< int > &	alloc,
		int	m
	)

allocate processors to rectangle proportionnally to their load.

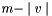This allocation is done using the following algorithm: $alloc[i] = \lceil \frac{load(v[i])*(m-\mid v\mid)}{load(psa)} \rceil$ . It might remain $m-\mid v\mid$ processors which are distributed greedily to the rectangle $v[i]$ which maximize $\frac{load(v[i])}{alloc[i]}$ .

Parameters:

	psa	a prefix sum array
	v	the set of rectangle to allocate processor to. v is assumed to cover the whole psa
	alloc	output vector for the number of number of processor per rectangle
	m	number of processors to distribute

TODO this should be done with a heap to reduce the complexity.

template<typename T , typename Pr >

int util::extractXDim	(	const util::RectList< T, Pr > &	currentP,
		int *	cuts
	)

Extracts first dimension cut points and puts them in an array. 2nd dimension cuts are also decomposed and put in a vector because 2nd dimension cuts can be variable size in m-way jagged partitions. This method assumes the input rectangle list is generated by a -HORF variant of jagged partitioning algorithm or a rectilinear algorithm.

Parameters:

`[in]`	currentP	Partition to be decomposed
`[out]`	cuts	Cut points of the 1st dim. the lenght of this array must be procX+1 which means top and bottom of the matrix also included (i.e 1,cut1,cut2,...,matrix_1st_dimension_size). This format follows 1D partitioning format with additional 2 cuts. To retrieve 1D partitioning format simply drop cuts[0] and cuts[procX]

Returns:: number of stripes in the currentP.

template<typename T , typename Pr >

int util::extractXDim	(	const util::RectList< T, Pr > &	currentP,
		int *	cuts,
		std::vector< int >	procs[]
	)

Extracts first dimension cut points and puts them in an array. 2nd dimension cuts are also decomposed and put in a vector because 2nd dimension cuts can be variable size in m-way jagged partitions. This method assumes the input rectangle list is generated by a -HORF variant of jagged partitioning algorithm or a rectilinear algorithm.

Parameters:

`[in]`	currentP	Partition to be decomposed
`[out]`	cuts	Cut points of the 1st dim. the lenght of this array must be procX+1 which means top and bottom of the matrix also included (i.e 1,cut1,cut2,...,matrix_1st_dimension_size). This format follows 1D partitioning format with additional 2 cuts. To retrieve 1D partitioning format simply drop cuts[0] and cuts[procX]
`[out]`	procs	procs[i] is the 2nd dimension cut points in the ith row.

Returns:: number of stripes in the currentP.

int util::intfactor ( int x )

finds the largest factor of a number less than its square root

std::ostream & util::operator<<	(	std::ostream &	out,
		const rectangle &	r
	)

template<typename T , typename Pr >

std::ostream & util::operator<<	(	std::ostream &	out,
		const util::RectList< T, Pr > &	r
	)

template<typename Pr , typename output >

void util::output_psa	(	const Pr &	psa,
		output &	out
	)

outputs the load array represented by a prefix sum array.

Parameters:

	psa	a 2d prefix sum array respecting the bracket notation described in util::PrefixSumArray2DOfTBracket
	out	a stream the array will be writen to

template<typename T >

void util::prefixsum	(	const T *	array,
		T *	result,
		int	length
	)

Assembles 1d prefix sum array.

Parameters:

`[in]`	array	Original 1d array instance
`[out]`	result	Output prefix sum array with result[0]=0 and result[i]=result[i-1]+array[i]
`[in]`	length	Original array's length

util Namespace Reference

Detailed Description

Classes

Functions

Function Documentation